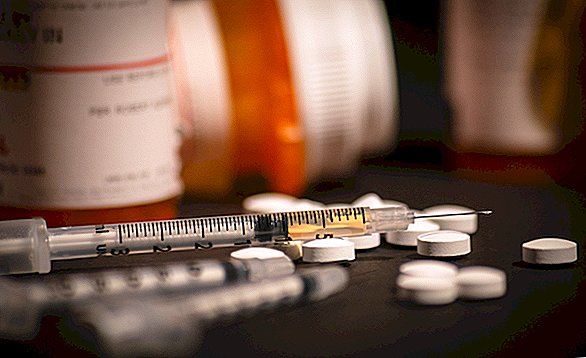
คำบรรยายภาพ: มุมมองของดวงจันทร์ที่ perigee และ apogee
ในฐานะครูฉันมักจะมองหาห้องทดลองที่มีการตั้งค่าง่าย ๆ ที่เหมาะสมสำหรับนักเรียน สิ่งที่ฉันโปรดปรานในปัจจุบันคือการค้นหาความเร็วของแสงด้วยช็อคโกแลต
ในกระดาษใหม่ที่อัปโหลดไปยัง arXiv เมื่อเร็ว ๆ นี้ Kevin Krisciunas จาก Texas A&M อธิบายถึงวิธีการกำหนดความประหลาดของวงโคจรของดวงจันทร์โดยมีข้อผิดพลาดต่ำอย่างน่าประหลาดใจโดยใช้ไม้เมตรและกระดาษแข็งและโปรแกรมสำหรับเส้นโค้งที่เหมาะสม ดาวแปรแสง
วิธีนี้ใช้ประโยชน์จากข้อเท็จจริงที่ว่าความเยื้องศูนย์กลางสามารถหาได้จากอัตราส่วนของขนาดเชิงมุมเฉลี่ยของวัตถุและครึ่งหนึ่งของแอมพลิจูด ดังนั้นวัตถุประสงค์หลักคือการวัดปริมาณทั้งสองนี้
กลยุทธ์ของเควินในการทำเช่นนี้คือการใช้ประโยชน์จากหลุมเจาะกระดาษแข็งซึ่งสามารถเลื่อนไปตามไม้เมตร โดยการจ้องมองผ่านรูที่ดวงจันทร์และเลื่อนการ์ดไปมาจนกว่าขนาดเชิงมุมของหลุมจะทับกันดวงจันทร์ จากนั้นเส้นผ่านศูนย์กลางของหลุมหารด้วยระยะทางลงที่แท่งมิเตอร์ทำให้ขนาดเชิงมุมต้องขอบคุณสูตรมุมเล็ก ๆ (? = d / D เป็นเรเดียนถ้า D >> d)
เพื่อป้องกันข้อผิดพลาดอย่างเป็นระบบในการพิจารณาผิดเนื่องจากการ์ดเลื่อนไปข้างหน้าจนกว่าขนาดของหลุมจะตรงกับดวงจันทร์มันเป็นการดีที่สุดที่จะเข้าหามันจากอีกทิศทางหนึ่ง มาจากในจากปลายสุดของแท่งมิเตอร์ สิ่งนี้จะช่วยลดข้อผิดพลาดและในความพยายามของเควินเขาพบว่าเขามีการแพร่กระจายทั่วไป± 4 มม. เมื่อทำเช่นนั้น
ณ จุดนี้ยังมีข้อผิดพลาดอีกอย่างเป็นระบบที่ต้องนำมาพิจารณา: นักเรียนมีขนาด จำกัด เทียบได้กับช่องมองเห็น นี่จะทำให้ขนาดเชิงมุมจริงต่ำเกินไป ดังนั้นจำเป็นต้องมีปัจจัยการแก้ไข
เพื่อให้ได้ปัจจัยการแก้ไขนี้เควินวางดิสก์ 91 มม. ที่ระยะ 10 เมตร (ซึ่งควรสร้างดิสก์ที่มีขนาดเชิงมุมเท่ากับดวงจันทร์เมื่อมองจากระยะไกล) เพื่อให้เกิดการจับคู่ที่ดีที่สุดแผ่นกระดาษแข็งที่มีรูที่เห็น ควร จำเป็นต้องวางที่ 681.3 มม. บนแท่งมิเตอร์ แต่เนื่องจากข้อผิดพลาดอย่างเป็นระบบของนักเรียนเควินพบว่าจำเป็นต้องอยู่ที่ 821 มม. อัตราส่วนของการจัดตำแหน่งที่สังเกตได้ต่อการจัดวางที่เหมาะสมนั้นให้ปัจจัยการแก้ไขที่เควินใช้ (1.205) สิ่งนี้จะต้องได้รับการปรับเทียบสำหรับแต่ละบุคคลและยังขึ้นอยู่กับปริมาณของแสงในช่วงเวลาของการสังเกตเนื่องจากสิ่งนี้จะส่งผลกระทบต่อเส้นผ่านศูนย์กลางของรูม่านตาด้วย อย่างไรก็ตามการใช้ปัจจัยการแก้ไขเดียวให้ผลลัพธ์ที่น่าพอใจ
ซึ่งจะช่วยให้สามารถนำข้อมูลที่ถูกต้องไปใช้เพื่อกำหนดปริมาณที่จำเป็น (ขนาดเฉลี่ยเชิงมุมและ 1/2 แอมพลิจูด) ในการพิจารณาสิ่งเหล่านี้เควินใช้โปรแกรมที่เรียกว่า PERDET ซึ่งออกแบบมาสำหรับการปรับเส้นโค้งไซนัสให้เหมาะสมกับการแกว่งในดาวแปรแสง โปรแกรมใดที่สามารถปรับให้พอดีกับส่วนโค้งดังกล่าวกับจุดข้อมูลโดยใช้ a?2 พอดีหรือการวิเคราะห์ฟูริเยร์จะเหมาะกับส่วนท้ายนี้
จากโปรแกรมดังกล่าวเมื่อกำหนดขนาดเชิงมุมและแอมพลิจูดครึ่งค่าเฉลี่ยแล้วอัตราส่วนของพวกมันจะให้ค่าความเยื้องศูนย์ สำหรับการทดลองของเควินเขาพบว่ามีค่า 0.039 ± 0.006 นอกจากนี้ระยะเวลาที่เขากำหนดจากผู้ให้บริการถึงผู้รับคือ 27.24 ± 0.29 วันซึ่งเป็นข้อตกลงที่ยอดเยี่ยมโดยมีมูลค่าที่ยอมรับได้ 27.55 วัน