คุณอาจต้องการใส่แว่นตาที่สงสัยและตั้งให้สูงสุดสำหรับแว่นตานี้ นักคณิตศาสตร์ชาวอิตาลีได้คิดค้นสูตรที่ซับซ้อนซึ่งมีความคล้ายคลึงกันที่น่าทึ่งเลียนแบบการหมุนของกาแลคซีกังหันโดยไม่ต้องใช้สสารมืด
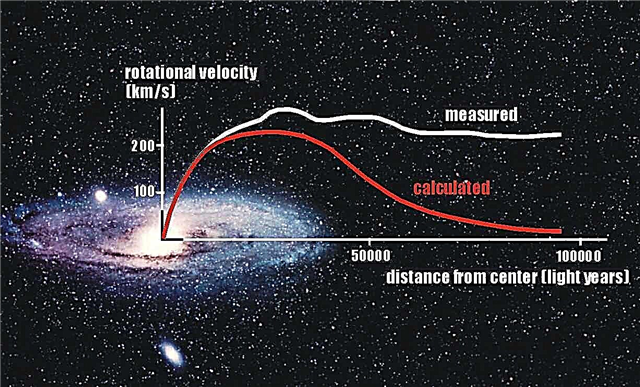
ปัจจุบันเส้นโค้งการหมุนกาแลคซีเหล่านี้แสดงถึงหลักฐานสำคัญสำหรับการมีอยู่ของสสารมืด - เนื่องจากดาวฤกษ์ชั้นนอกของกาแลคซีหมุนรอบตัวมักจะเคลื่อนที่ไปรอบ ๆ ดิสก์กาแลคซีอย่างรวดเร็วจนพวกมันควรบินออกไปในอวกาศ ในกาแลคซีเพื่อโน้มถ่วงพวกมันไว้ในวงโคจรของพวกเขา
สามารถชื่นชมปัญหานี้ได้โดยพิจารณาการเคลื่อนที่ของดาวเคราะห์ Keplerian ในระบบสุริยะของเรา ดาวพุธโคจรรอบดวงอาทิตย์ด้วยความเร็ววงโคจร 48 กิโลเมตรต่อวินาทีในขณะที่ดาวเนปจูนโคจรรอบดวงอาทิตย์ด้วยความเร็ววงโคจร 5 กิโลเมตรต่อวินาที ในระบบสุริยจักรวาลความใกล้ชิดของดาวเคราะห์กับมวลดวงอาทิตย์เป็นฟังก์ชันของความเร็วการโคจร ดังนั้นถ้าสมมุติว่ามวลของดวงอาทิตย์ลดลงความเร็วของวงโคจรของเนปจูนจะเคลื่อนตัวมันออกจากวงโคจรปัจจุบัน - อาจเหวี่ยงมันออกไปสู่อวกาศระหว่างดวงดาวถ้าการเปลี่ยนแปลงมีความสำคัญมากพอ
ฟิสิกส์ของกาแล็กซีทางช้างเผือกนั้นแตกต่างจากระบบสุริยะเนื่องจากมวลของมันถูกกระจายไปทั่วดิสก์กาแลคซีมากกว่า 99% ของมวลของมันที่กระจุกตัวอยู่ตรงกลาง - วิธีที่มันอยู่ในระบบสุริยะ
อย่างไรก็ตามในบทความ Space Magazine ที่ผ่านมาอธิบายว่าถ้าเราถือว่าความสัมพันธ์ที่คล้ายกันระหว่างมวลทางช้างเผือกและความเร็วการโคจรรอบดาวฤกษ์ชั้นนอกของมันเราต้องยอมรับว่าวัตถุที่มองเห็นได้ในทางช้างเผือกนั้นมีเพียง 10-20% ของมวลที่จำเป็นต้องมีความเร็วการโคจรของดาวฤกษ์ในดิสก์ชั้นนอก ดังนั้นเราจึงสรุปได้ว่าส่วนที่เหลือของมวลกาแลคซีนั้นจะต้องเป็นสสารมืด (มองไม่เห็น)
นี่เป็นมุมมองที่เป็นฉันทามติร่วมสมัยเกี่ยวกับการทำงานของกาแลคซี - และเป็นองค์ประกอบสำคัญของแบบจำลองมาตรฐานจักรวาลจักรวาลในปัจจุบัน แต่การาติได้มาพร้อมกับแนวคิดที่ดูเหมือนไม่น่าเชื่อว่ากาแลคซีหมุนวนสามารถอธิบายได้ด้วยอิทธิพลความโน้มถ่วงของสสารที่อยู่ไกลออกไปโดยไม่จำเป็นต้องดึงดูดสสารมืด

แนวคิดความคิดนั้นสมเหตุสมผลดี การวางตำแหน่งมวลที่มีนัยสำคัญแรงโน้มถ่วงนอกวงโคจรของดาวอาจดึงพวกมันออกสู่วงโคจรที่กว้างขึ้น แต่มันก็ยากที่จะดูว่าทำไมสิ่งนี้จึงเพิ่มความเร็วในการโคจรของพวกมัน การวาดวัตถุเข้าสู่วงโคจรที่กว้างขึ้นนั้นจะส่งผลให้มันต้องใช้เวลาในการโคจรรอบกาแลคซีนานขึ้นเนื่องจากมันจะมีเส้นรอบวงครอบคลุมมากขึ้น สิ่งที่เราเห็นโดยทั่วไปในกาแลคซีกังหันคือดาวฤกษ์ชั้นนอกโคจรรอบกาแลคซีในช่วงเวลาเดียวกับดาวเข้าด้านในมากขึ้น
แต่ถึงแม้ว่ากลไกที่เสนอนั้นดูเหมือนจะเป็นไปไม่ได้ แต่สิ่งที่น่าทึ่งเกี่ยวกับการเรียกร้องของ Carati ก็คือคณิตศาสตร์เห็นได้ชัดว่าส่งโค้งการหมุนกาแลคซีที่ใกล้เคียงกับค่าที่สังเกตเห็นอย่างมากของกาแลคซีที่รู้จักสี่แห่ง แน่นอนคณิตศาสตร์ให้พอดีอย่างใกล้ชิดเป็นพิเศษ
เมื่อใช้แว่นตาที่มีข้อกังขาอย่างแน่นหนาข้อสรุปต่อไปนี้อาจมาจากการค้นพบนี้:
•มีกาแลคซีจำนวนมากอยู่ข้างนอกนั่นไม่ใช่เรื่องยากที่จะหากาแลคซีสี่แห่งที่เหมาะสมกับคณิตศาสตร์
•คณิตศาสตร์ได้รับการติดตั้งย้อนยุคเพื่อให้ตรงกับข้อมูลที่สังเกตได้แล้ว
•คณิตศาสตร์ไม่ทำงาน หรือ
•ในขณะที่การตีความข้อมูลของผู้เขียนอาจใช้สำหรับการอภิปราย แต่คณิตศาสตร์นั้นใช้งานได้จริง
คณิตศาสตร์ใช้หลักการที่กำหนดขึ้นในสมการสนามไอน์สไตน์ซึ่งเป็นปัญหาในขณะที่สมการภาคสนามตั้งอยู่บนหลักการทางจักรวาลวิทยาซึ่งสันนิษฐานว่าผลกระทบของสสารที่อยู่ไกลออกไปนั้นน้อยมาก
กระดาษของ Carati ยังบันทึกอีกสองตัวอย่างที่คณิตศาสตร์สามารถใส่กาแลคซีที่มีความเร็วการหมุนลดลงในดาวชั้นนอก สิ่งนี้ทำได้โดยการเปลี่ยนสัญลักษณ์ของหนึ่งในองค์ประกอบของสูตร (ซึ่งอาจเป็น + หรือ -) ดังนั้นในแง่หนึ่งผลของสสารที่อยู่ไกลออกไปก็คือทำให้เกิดแรงดันบวกที่มีการหมุนอย่างรวดเร็วของดาวป้องกันไม่ให้มันบินออกไป - และในทางกลับกันมันสามารถเหนี่ยวนำให้เกิดแรงดันลบเพื่อกระตุ้นการสลายตัวผิดปกติ โค้งการหมุนของกาแลคซี
ตามที่พูดไปถ้าสิ่งที่ดูเหมือนจะดีเกินจริง - มันอาจไม่จริง ความคิดเห็นทั้งหมดยินดีต้อนรับ
อ่านเพิ่มเติม:
ผลกระทบแรงโน้มถ่วงของ Carati จากสสารที่อยู่ไกลออกไปบนเส้นโค้งการหมุนของกาแลคซีกังหัน