ให้เราคุยเกี่ยวกับธรรมชาติของจักรวาล การเข้าสู่การสนทนาเกี่ยวกับจักรวาลโดยรวมคุณจะจินตนาการถึงเรื่องราวที่เต็มไปด้วยเหตุการณ์มหัศจรรย์เช่นการล่มสลายของดวงดาวการชนทางช้างเผือกเหตุการณ์ประหลาดที่เกิดขึ้นกับอนุภาคและการระเบิดของพลังงานอย่างหายนะ คุณอาจคาดหวังว่าเรื่องราวจะยืดความกว้างของเวลาตามที่เราเข้าใจเริ่มจากบิ๊กแบงและเชื่อมโยงไปถึงคุณที่นี่ดวงตาของคุณเปียกโชกในโฟตอนที่ถูกปล่อยออกมาจากหน้าจอของคุณ แน่นอนว่าเป็นเรื่องราวที่ยิ่งใหญ่ แต่มีอีกด้านหนึ่งของการจัดประเภทที่น่าทึ่งของเหตุการณ์ที่มักถูกมองข้าม นั่นคือจนกว่าคุณจะพยายามเข้าใจสิ่งที่เกิดขึ้นจริง ๆ เบื้องหลังการรับรู้ที่น่าอัศจรรย์เหล่านี้มีกลไกในการทำงานที่ช่วยให้เราค้นพบทุกสิ่งที่คุณสนุกกับการเรียนรู้ กลไกนั้นคือคณิตศาสตร์และหากปราศจากมันจักรวาลก็ยังคงถูกปกคลุมไปด้วยความมืด ในบทความนี้ฉันจะพยายามโน้มน้าวคุณว่าคณิตศาสตร์ไม่ใช่ภารกิจทางจิตใจและไร้ประโยชน์บางครั้งที่สังคมสร้างมันขึ้นมาและแสดงให้คุณเห็นว่าเป็นภาษาที่เราใช้สื่อสารกับดวงดาว
ขณะนี้เราผูกพันกับระบบสุริยะของเรา คำพูดนี้ดีกว่าฟังดูจริง ๆ เนื่องจากการถูกผูกไว้กับระบบสุริยะของเรานั้นเป็นขั้นตอนสำคัญหนึ่งที่เพิ่มขึ้นจากการถูกผูกไว้กับโลกของเราอย่างที่เราเป็น
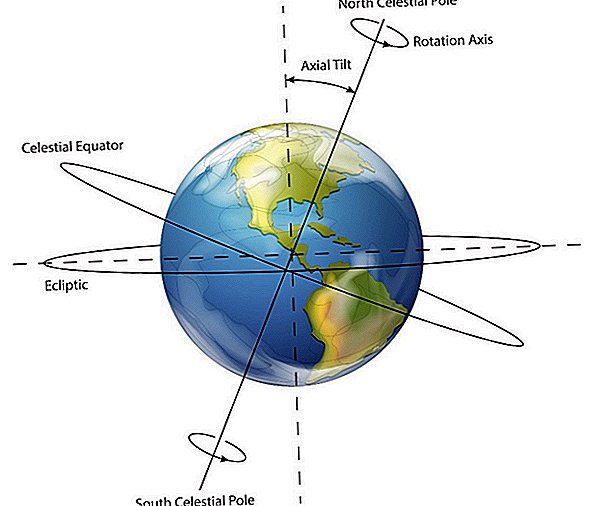
ก่อนที่จิตใจที่สำคัญบางอย่างเลือกที่จะเปลี่ยนอัจฉริยะของพวกเขาไปสู่สวรรค์ ก่อนหน้าคนอย่างกาลิเลโอผู้เล็งกล้องสอดแนมขึ้นสู่ท้องฟ้าหรือเคปเลอร์ค้นพบว่าดาวเคราะห์เคลื่อนที่รอบดวงอาทิตย์ในวงรีหรือนิวตันค้นพบความโน้มถ่วงคงตัวคณิตศาสตร์ค่อนข้าง จำกัด และความเข้าใจของเราเกี่ยวกับจักรวาลค่อนข้างไม่รู้ ที่แกนกลางของมันคณิตศาสตร์อนุญาตให้สปีชีส์ที่ถูกผูกไว้กับระบบสุริยะของมันสามารถตรวจสอบความลึกของจักรวาลจากด้านหลังโต๊ะ ตอนนี้เพื่อชื่นชมความมหัศจรรย์ที่เป็นคณิตศาสตร์เราต้องย้อนกลับไปก่อนและดูจุดเริ่มต้นสั้น ๆ และเชื่อมโยงเข้ากับการดำรงอยู่ของเราได้อย่างไร
คณิตศาสตร์มาจากเผ่ามนุษย์ยุคแรก ๆ มาก่อนแน่นอน (ก่อนที่จะมีวัฒนธรรมของชาวบาบิโลนซึ่งมีสาเหตุมาจากคณิตศาสตร์ที่จัดเป็นครั้งแรกในประวัติศาสตร์ที่บันทึกไว้) ซึ่งอาจใช้คณิตศาสตร์เป็นวิธีการติดตามวัฏจักรทางจันทรคติหรือสุริยจักรวาล สัตว์อาหารและ / หรือผู้คนโดยผู้นำ มันเป็นเรื่องธรรมชาติเหมือนตอนที่คุณยังเป็นเด็กและคุณจะเห็นว่าคุณมี

หนึ่งของเล่นบวกอีกหนึ่งของเล่นหมายความว่าคุณมีมากกว่าหนึ่งของเล่น เมื่อคุณโตขึ้นคุณจะพัฒนาความสามารถในการมองเห็นว่า 1 + 1 = 2 และเลขคณิตแบบง่าย ๆ ดูเหมือนจะถูกรวมเข้ากับธรรมชาติของเรา คนที่ยอมรับว่าพวกเขาไม่ได้มีความคิดด้านคณิตศาสตร์ถูกเข้าใจผิดอย่างน่าเศร้าเพราะในขณะที่เราทุกคนมีใจสำหรับการหายใจหรือกระพริบตาเราทุกคนมีความสามารถโดยธรรมชาตินี้ที่จะเข้าใจเลขคณิต คณิตศาสตร์เป็นทั้งเหตุการณ์ธรรมชาติและระบบที่มนุษย์ออกแบบขึ้น ดูเหมือนว่าธรรมชาติทำให้เรามีความสามารถนี้ในการจดจำรูปแบบในรูปแบบของเลขคณิตและจากนั้นเราก็สร้างระบบคณิตศาสตร์ที่ซับซ้อนมากขึ้นซึ่งไม่ชัดเจนในธรรมชาติ แต่ให้เราสื่อสารกับธรรมชาติเพิ่มเติม
ทั้งหมดนี้นอกเหนือจากคณิตศาสตร์ที่พัฒนาควบคู่ไปกับการพัฒนามนุษย์และดำเนินไปในทำนองเดียวกันกับแต่ละวัฒนธรรมที่พัฒนาขึ้นพร้อมกัน เป็นข้อสังเกตที่ยอดเยี่ยมที่ได้เห็นว่าวัฒนธรรมที่ไม่มีการติดต่อซึ่งกันและกันกำลังพัฒนาโครงสร้างทางคณิตศาสตร์ที่คล้ายกันโดยไม่ต้องพูดคุยกัน อย่างไรก็ตามมันไม่ได้จนกว่ามนุษยชาติจะเปลี่ยนความสงสัยทางคณิตศาสตร์ของพวกเขาไปสู่ท้องฟ้าว่าคณิตศาสตร์เริ่มพัฒนาอย่างน่าอัศจรรย์อย่างแท้จริง มันไม่ใช่เรื่องบังเอิญเลยที่การปฏิวัติทางวิทยาศาสตร์ของเราได้รับการกระตุ้นโดยการพัฒนาคณิตศาสตร์ขั้นสูงที่สร้างขึ้นไม่ให้แกะหรือผู้คนนับ แต่จะเพิ่มความเข้าใจของเราเกี่ยวกับสถานที่ของเราในจักรวาล เมื่อกาลิเลโอเริ่มวัดอัตราที่วัตถุตกหลุมในความพยายามที่จะแสดงทางคณิตศาสตร์ว่ามวลของวัตถุนั้นเกี่ยวข้องกับความเร็วที่มันตกลงมาน้อยมากอนาคตของมนุษยชาติจะเปลี่ยนแปลงตลอดไป
นี่คือสิ่งที่มุมมองของจักรวาลเชื่อมโยงกับความต้องการของเราในการเพิ่มเติมความรู้ทางคณิตศาสตร์ของเรา หากไม่ใช่เพื่อการคำนวณเราก็ยังคงคิดว่าเราอยู่บนดาวเคราะห์ดวงหนึ่งในไม่กี่ดวงที่โคจรรอบดาวฤกษ์ท่ามกลางฉากหลังของแสงที่ไม่เคลื่อนไหว นี่เป็นภาพที่ค่อนข้างเยือกเย็นในวันนี้เมื่อเทียบกับสิ่งที่เรารู้
เกี่ยวกับจักรวาลขนาดใหญ่ที่น่ากลัวที่เราอาศัยอยู่ความคิดเกี่ยวกับจักรวาลนี้กระตุ้นให้เราเข้าใจมากขึ้นเกี่ยวกับคณิตศาสตร์สามารถถูกจารึกไว้ในวิธีที่โยฮันเนสเคปเลอร์ใช้สิ่งที่เขาสังเกตการณ์ดาวเคราะห์ทำแล้วนำคณิตศาสตร์มาพัฒนารูปแบบที่ค่อนข้างแม่นยำ วิธีการทำนายการเคลื่อนที่ของดาวเคราะห์) ของระบบสุริยจักรวาล นี่เป็นหนึ่งในการสาธิตมากมายที่แสดงให้เห็นถึงความสำคัญของคณิตศาสตร์ในประวัติศาสตร์ของเราโดยเฉพาะในด้านดาราศาสตร์และฟิสิกส์
เรื่องราวของคณิตศาสตร์ยิ่งน่าทึ่งยิ่งขึ้นเมื่อเราผลักดันให้เป็นหนึ่งในนักคิดขั้นสูงที่เป็นที่รู้จักที่สุด เซอร์ไอแซกนิวตันเมื่อไตร่ตรองถึงการเคลื่อนที่ของดาวหางฮัลเลย์มาถึงการตระหนักว่าคณิตศาสตร์ที่ใช้มาจนถึงปัจจุบันเพื่ออธิบายการเคลื่อนที่ของวัตถุขนาดใหญ่
ร่างกายก็คงไม่พอเพียงถ้าเราจะเข้าใจอะไรนอกเหนือไปจากซอกสวรรค์ที่ดูเหมือนจะ จำกัด ในการแสดงความฉลาดบริสุทธิ์ที่ให้เหตุผลกับคำแถลงก่อนหน้านี้ของฉันเกี่ยวกับวิธีที่เราสามารถนำสิ่งที่เรามีตามธรรมชาติมาสร้างระบบที่ซับซ้อนมากขึ้นนิวตันพัฒนาแคลคูลัสซึ่งวิธีนี้ใกล้กับวัตถุเคลื่อนที่เขาสามารถแม่นยำ จำลองการเคลื่อนที่ของดาวหางของ Halley ไม่เพียงเท่านั้น แต่ยังรวมถึงร่างสวรรค์อื่น ๆ ที่เคลื่อนที่ข้ามท้องฟ้า
ในทันทีทันใดจักรวาลของเราทั้งคู่เปิดตัวต่อหน้าเราปลดล็อคความสามารถแทบไม่ จำกัด สำหรับเราที่จะพูดคุยกับจักรวาลอย่างที่ไม่เคยมีมาก่อน นิวตันยังขยายตัวตามสิ่งที่เคปเลอร์เริ่ม Newton ยอมรับว่าสมการทางคณิตศาสตร์ของ Kepler สำหรับการเคลื่อนที่ของดาวเคราะห์กฎข้อที่ 3 ของ Kepler (P2= a3 ) มีพื้นฐานมาจากการสังเกตเชิงประจักษ์อย่างหมดจดและมีไว้เพื่อวัดสิ่งที่เราสังเกตเห็นภายในระบบสุริยะของเราเท่านั้น ความฉลาดทางคณิตศาสตร์ของนิวตันคือการตระหนักว่าสมการพื้นฐานนี้สามารถทำให้เป็นสากลได้โดยการใช้ค่าความโน้มถ่วงคงที่กับสมการซึ่งให้กำเนิดสมการที่สำคัญที่สุดอย่างหนึ่งที่มนุษย์จะได้รับ กฎข้อที่สามของเคปเลอร์เวอร์ชันของนิวตัน
สิ่งที่นิวตันรู้ก็คือเมื่อสิ่งต่าง ๆ เคลื่อนที่ในลักษณะที่ไม่ใช่เชิงเส้นการใช้พีชคณิตพื้นฐานจะไม่ให้คำตอบที่ถูกต้อง ในที่นี้วางหนึ่งในความแตกต่างที่สำคัญระหว่างพีชคณิตและแคลคูลัส พีชคณิตช่วยให้เราสามารถค้นหาความชัน (อัตราการเปลี่ยนแปลง) ของเส้นตรง (อัตราการเปลี่ยนแปลงคงที่) ในขณะที่แคลคูลัสอนุญาตให้หนึ่งค้นหาความชันของเส้นโค้ง (อัตราการเปลี่ยนแปลงของการเปลี่ยนแปลง) เห็นได้ชัดว่ามีแอปพลิเคชั่นมากมายของแคลคูลัสมากกว่าแค่นี้ แต่ฉันแค่แสดงให้เห็นถึงความแตกต่างพื้นฐานระหว่างทั้งสองเพื่อแสดงให้คุณเห็นว่าการปฏิวัติแนวคิดใหม่นี้เป็นอย่างไร ทั้งหมดในครั้งเดียวการเคลื่อนที่ของดาวเคราะห์และวัตถุอื่น ๆ ที่โคจรรอบดวงอาทิตย์สามารถวัดได้อย่างแม่นยำมากขึ้นและทำให้เรามีความสามารถในการเข้าใจจักรวาลได้ลึกขึ้นเล็กน้อย การอ้างถึงกฎข้อที่สามของ Kepler เวอร์ชัน Netwon ตอนนี้เราสามารถใช้ (และยังคงทำ) สมการทางฟิสิกส์ที่น่าทึ่งนี้กับทุกสิ่งที่กำลังโคจรอยู่อย่างอื่น จากสมการนี้เราสามารถกำหนดมวลของวัตถุใดวัตถุหนึ่งได้ระยะห่างจากกันแรงของแรงโน้มถ่วงที่กระทำระหว่างวัตถุทั้งสองและคุณสมบัติทางกายภาพอื่น ๆ ที่สร้างขึ้นจากการคำนวณอย่างง่ายเหล่านี้
ด้วยความเข้าใจในคณิตศาสตร์ของเขานิวตันสามารถหาค่าคงตัวโน้มถ่วงดังกล่าวสำหรับวัตถุทั้งหมดในจักรวาล (G = 6.672 × 10-11 ม2 กิโลกรัม-2 ) ค่าคงที่นี้ทำให้เขาสามารถรวมดาราศาสตร์และฟิสิกส์เข้าด้วยกันซึ่งทำให้เกิดการคาดการณ์เกี่ยวกับสิ่งที่เคลื่อนไหวในเอกภพ ตอนนี้เราสามารถวัดมวลของดาวเคราะห์ (และดวงอาทิตย์) ได้แม่นยำมากขึ้นตามฟิสิกส์ของนิวตัน (ชื่อที่เหมาะสมเพื่อเป็นเกียรติแก่ความสำคัญของนิวตันที่อยู่ภายในฟิสิกส์และคณิตศาสตร์) ตอนนี้เราสามารถใช้ภาษาที่ค้นพบใหม่นี้กับจักรวาลและเริ่มบังคับให้เปิดเผยความลับของมัน นี่เป็นช่วงเวลาที่กำหนดไว้สำหรับมนุษยชาติในสิ่งเหล่านั้นทั้งหมดที่ห้ามไม่ให้เราเข้าใจก่อนที่คณิตศาสตร์รูปแบบใหม่นี้จะอยู่ที่ปลายนิ้วของเราพร้อมที่จะค้นพบ นี่คือความฉลาดของการเข้าใจแคลคูลัสซึ่งคุณกำลังพูดภาษาของดวงดาว
อาจไม่มีภาพประกอบที่ดีขึ้นของพลังที่คณิตศาสตร์มอบให้เราในการค้นพบดาวเคราะห์เนปจูน จนกระทั่งค้นพบในเดือนกันยายน ค.ศ. 1846 ดาวเคราะห์ถูกค้นพบอย่างง่าย ๆ โดยการสังเกต“ ดาว” บางดวงที่เคลื่อนที่ไปตามฉากหลังของดาวดวงอื่น ๆ ทั้งหมดด้วยวิธีแปลก ๆ คำว่าดาวเคราะห์เป็นภาษากรีกสำหรับ "ผู้หลงทาง" ซึ่งดาวประหลาดเหล่านี้ได้เดินทางข้ามท้องฟ้าในรูปแบบที่สังเกตเห็นได้ในเวลาต่าง ๆ ของปี เมื่อกล้องโทรทรรศน์กาลิเลโอหันขึ้นสู่ท้องฟ้าเป็นครั้งแรกผู้ที่หลงทางเหล่านี้ก็เข้าสู่โลกอื่นที่ดูเหมือนจะเป็นของเรา ถ้าความจริงโลกบางแห่งดูเหมือนจะเป็นระบบสุริยะเล็ก ๆ น้อย ๆ เองอย่างที่กาลิเลโอค้นพบเมื่อเขาเริ่มบันทึกดวงจันทร์ของดาวพฤหัสเมื่อพวกมันโคจรรอบโลก
หลังจากนิวตันนำเสนอสมการทางฟิสิกส์ของเขาไปทั่วโลกนักคณิตศาสตร์ก็พร้อมและตื่นเต้นที่จะเริ่มใช้มันกับสิ่งที่เราติดตามมานานหลายปี ราวกับว่าเรากระหายความรู้และในที่สุดก็มีคนเปิดก๊อกน้ำ เราเริ่มวัดการเคลื่อนที่ของดาวเคราะห์และได้แบบจำลองที่แม่นยำยิ่งขึ้นสำหรับพฤติกรรมของพวกเขา เราใช้สมการเหล่านี้เพื่อประมาณมวลของดวงอาทิตย์ เราสามารถคาดการณ์ที่น่าทึ่งซึ่งได้รับการตรวจสอบครั้งแล้วครั้งเล่าโดยการสังเกต สิ่งที่เราทำคือไม่เคยมีมาก่อนเนื่องจากเราใช้คณิตศาสตร์เพื่อทำให้แทบเป็นไปไม่ได้ที่จะรู้คำทำนายว่าคุณจะคิดว่าเราไม่สามารถทำได้หากไม่ได้ไปที่ดาวเคราะห์เหล่านี้จริง ๆ แล้วใช้การสังเกตจริงเพื่อพิสูจน์คณิตศาสตร์ที่ถูกต้อง อย่างไรก็ตามสิ่งที่เราทำก็เริ่มเข้าใจความแตกต่างแปลก ๆ กับบางสิ่ง ยกตัวอย่างเช่นดาวยูเรนัสไม่ได้ทำงานอย่างที่ควรเป็นตามกฎหมายของนิวตัน

สิ่งที่ทำให้การค้นพบดาวเนปจูนน่าอัศจรรย์มากคือลักษณะที่ค้นพบ สิ่งที่นิวตันทำก็คือการเปิดเผยภาษาที่ลึกซึ้งของจักรวาลซึ่งเอกภพสามารถเปิดเผยเราได้มากขึ้น และนี่คือสิ่งที่เกิดขึ้นเมื่อเราใช้ภาษานี้กับวงโคจรของดาวยูเรนัส ลักษณะที่ดาวยูเรนัสโคจรอยู่นั้นน่าสงสัยและไม่เหมาะกับสิ่งที่มันควรจะเป็นถ้ามันเป็นดาวเคราะห์ดวงเดียวที่อยู่ห่างไกลจากดวงอาทิตย์ เมื่อมองดูตัวเลขมันจะต้องมีสิ่งอื่นที่รบกวนวงโคจรของมัน ตอนนี้ก่อนความเข้าใจและกฎทางคณิตศาสตร์ของนิวตันเราคงไม่มีเหตุผลที่จะสงสัยว่ามีอะไรผิดปกติในสิ่งที่เราสังเกต ดาวยูเรนัสโคจรตามวิถียูเรนัส มันเป็นอย่างที่มันเป็น แต่เมื่อเราถามคำถามในรูปแบบที่ถูกต้องเรากลับมาทบทวนอีกครั้งว่าความคิดทางคณิตศาสตร์เป็นบทสนทนาที่เพิ่มขึ้นเรื่อย ๆ เมื่อเราถามคำถามในรูปแบบที่ถูกต้อง นี่คือความงามของคณิตศาสตร์ที่มีขนาดใหญ่ การสนทนาอย่างต่อเนื่องกับจักรวาลซึ่งเกินกว่าที่เราจะคาดหวังได้ถูกเปิดเผย
มันมาถึงนักคณิตศาสตร์ชาวฝรั่งเศส Urbain Le Verrier ผู้ซึ่งนั่งลงและทำงานอย่างระมัดระวังผ่านสมการทางคณิตศาสตร์ของวงโคจรของดาวยูเรนัส สิ่งที่เขาทำคือใช้สมการทางคณิตศาสตร์ของนิวตันย้อนกลับโดยตระหนักว่าต้องมีวัตถุนอกวงโคจรของดาวยูเรนัสที่โคจรรอบดวงอาทิตย์ด้วย
และจากนั้นจึงมองหาการใช้มวลและระยะทางที่ถูกต้องซึ่งวัตถุที่มองไม่เห็นนี้จำเป็นสำหรับการรบกวนวงโคจรของดาวยูเรนัสในแบบที่เราสังเกตเห็น นี่เป็นปรากฎการณ์เพราะเราใช้แผ่นหนังและหมึกเพื่อค้นหาดาวเคราะห์ที่ไม่มีใครสังเกตเห็นจริง ๆ สิ่งที่เขาค้นพบก็คือวัตถุในไม่ช้าที่จะเป็นเนปจูนจะต้องโคจรอยู่ในระยะห่างจากดวงอาทิตย์โดยเฉพาะกับมวลเฉพาะที่จะทำให้เกิดความผิดปกติในเส้นทางการโคจรของดาวยูเรนัส ด้วยความมั่นใจในการคำนวณทางคณิตศาสตร์ของเขาเขาได้นำตัวเลขของเขาไปยัง New Berlin Observatory ซึ่งนักดาราศาสตร์ Johann Gottfried Galle มองตรงที่การคำนวณของ Verrier บอกให้เขาดูและมีการวางดาวเคราะห์ดวงที่ 8 และสุดท้ายของระบบสุริยะของเรา จากที่การคำนวณของ Verrier บอกให้เขามอง สิ่งที่เพิ่งเกิดขึ้นคือการยืนยันทฤษฎีความโน้มถ่วงของนิวตันอย่างไม่น่าเชื่อและพิสูจน์ว่าคณิตศาสตร์ของเขาถูกต้อง

ข้อมูลเชิงลึกทางคณิตศาสตร์ประเภทนี้ยังคงดำเนินต่อไปอีกนานหลังจากที่นิวตัน ในที่สุดเราก็เริ่มเรียนรู้เกี่ยวกับจักรวาลมากขึ้นด้วยการถือกำเนิดของเทคโนโลยีที่ดีกว่า (เกิดจากความก้าวหน้าทางคณิตศาสตร์) ขณะที่เราย้ายเข้าสู่ศตวรรษที่ 20 ทฤษฎีควอนตัมเริ่มเป็นรูปเป็นร่างขึ้นและในไม่ช้าเราก็ตระหนักว่าฟิสิกส์และคณิตศาสตร์ของนิวตันดูเหมือนจะไม่มีผลใด ๆ ต่อสิ่งที่เราสังเกตเห็นในระดับควอนตัม ในเหตุการณ์สำคัญอีกเหตุการณ์หนึ่งในประวัติศาสตร์ของมนุษย์ แต่นำเสนอโดยความก้าวหน้าทางคณิตศาสตร์อีกครั้ง Albert Einstein เปิดเผยทฤษฎีของเขาเกี่ยวกับทฤษฎีสัมพัทธภาพทั่วไปและทฤษฎีสัมพัทธภาพพิเศษซึ่งเป็นวิธีใหม่ในการมองไม่เพียง แต่แรงโน้มถ่วงเท่านั้น

ยังเกี่ยวกับพลังงานและจักรวาลโดยทั่วไป สิ่งที่คณิตศาสตร์ของ Einstein ทำนั้นช่วยให้เราค้นพบการสนทนาที่ลึกซึ้งยิ่งขึ้นกับจักรวาลอีกครั้งซึ่งเราเริ่มเข้าใจต้นกำเนิดของมัน
การดำเนินการตามแนวโน้มของการพัฒนาความเข้าใจของเราต่อไปสิ่งที่เราได้ตระหนักคือตอนนี้มีสองสาขาของฟิสิกส์ที่ไม่สอดคล้องกันทั้งหมด ฟิสิกส์ของนิวตันหรือ“ คลาสสิก” ที่ใช้งานได้ดีเป็นพิเศษกับการเคลื่อนที่ของดาวเคราะห์กาแลกซี่และฟิสิกส์ควอนตัมที่อธิบายขนาดเล็กมาก (ปฏิกิริยาของอนุภาคย่อยอะตอมแสง ฯลฯ ) ปัจจุบันฟิสิกส์สองส่วนนี้ไม่ได้อยู่ในแนวเดียวกันเหมือนกับภาษาถิ่นสองภาษา พวกมันเหมือนกันและทำงานทั้งคู่ แต่พวกมันกลับไม่สามารถตกลงกันได้อย่างง่ายดาย หนึ่งในความท้าทายที่ยิ่งใหญ่ที่สุดที่เราเผชิญอยู่ในวันนี้คือการพยายามสร้าง“ ทฤษฎีของทุกสิ่ง” ที่ยิ่งใหญ่ทางคณิตศาสตร์ซึ่งรวมกันกฎหมายในโลกควอนตัมกับโลกที่ใหญ่โตหรือเพื่ออธิบายทุกอย่างในแง่ของกลศาสตร์ควอนตัม นี่ไม่ใช่งานง่าย แต่เรามุ่งมั่นไปข้างหน้าอย่างไรก็ตาม
อย่างที่คุณเห็นคณิตศาสตร์เป็นมากกว่าชุดของสมการที่คลุมเครือและกฎที่ซับซ้อนที่คุณต้องจดจำ คณิตศาสตร์เป็นภาษาของจักรวาลและในการเรียนรู้ภาษานี้คุณกำลังเปิดตัวกลไกหลักที่จักรวาลใช้ มันเหมือนกับการเดินทางไปยังดินแดนใหม่และค่อยๆหยิบภาษาพื้นเมืองขึ้นมาเพื่อที่คุณจะได้เริ่มเรียนรู้จากพวกเขา ความพยายามทางคณิตศาสตร์นี้คือสิ่งที่ช่วยให้เราซึ่งเป็นสปีชีส์ที่ถูกผูกไว้กับระบบสุริยะของเราเพื่อสำรวจความลึกของจักรวาล ณ ตอนนี้ไม่มีทางที่เราจะเดินทางไปยังใจกลางกาแลคซีของเราและสังเกตหลุมดำมวลมหาศาลที่นั่นเพื่อยืนยันการมีอยู่ของมัน ไม่มีทางที่เราจะเข้าสู่เนบิวลามืดและเฝ้าดูดวงดาวที่เกิดขึ้นในแบบเรียลไทม์ กระนั้นผ่านคณิตศาสตร์เราสามารถเข้าใจว่าสิ่งเหล่านี้มีอยู่จริงและทำงานอย่างไร เมื่อคุณเริ่มที่จะเรียนรู้คณิตศาสตร์คุณไม่เพียง แต่จะขยายความคิดของคุณ แต่คุณกำลังเชื่อมต่อกับจักรวาลในระดับพื้นฐาน คุณสามารถสำรวจฟิสิกส์สุดเจ๋งที่ขอบฟ้าเหตุการณ์ของหลุมดำหรือเป็นพยานต่อความโกรธแค้นที่ทำลายล้างหลังซูเปอร์โนวาจากโต๊ะของคุณ ทุกสิ่งที่ฉันกล่าวถึงในตอนต้นของบทความนี้มุ่งเน้นผ่านคณิตศาสตร์ เรื่องราวที่ยิ่งใหญ่ของจักรวาลเขียนขึ้นในวิชาคณิตศาสตร์และความสามารถของเราในการแปลตัวเลขเหล่านั้นเป็นเหตุการณ์ที่เราทุกคนรักที่จะเรียนรู้เกี่ยวกับไม่มีอะไรน่าพิศวง ดังนั้นจำไว้ว่าเมื่อคุณได้รับโอกาสในการเรียนรู้คณิตศาสตร์ให้ยอมรับทุก ๆ ส่วนเพราะคณิตศาสตร์เชื่อมต่อเรากับดวงดาว